角度から三角関数(sin・cos・tan)の値を求めるツール
WEBブラウザ上で入力された角度から正弦(sin)・余弦(cos)・正接(tan)の値を求めるツールです。
三角関数の意味と使い方の解説付き。
三角関数の意味と使い方の解説付き。
ツールの使用説明
上の欄に三角関数を取得したい角度をを入力して「計算」ボタンを押してください。
すると、下の欄にsin・cos・tanの値が表示されます。
すると、下の欄にsin・cos・tanの値が表示されます。
三角関数とは?
三角形が相似となる条件は以下の3つです。
直角三角形の場合は1つの角の大きさが90°で確定しているため、残り1つの鋭角の角度を決定するだけでそれに対応して三角形の3辺の比も決定されるということになります。
この直角三角形の鋭角と3辺の比の関係を関数化したものが「三角関数」です。
・3組の辺の比が等しい
・2組の角の大きさが等しい
・2組の辺の比とその間の角の大きさが等しい
この条件より「2組の角の大きさが等しい三角形は3辺の比も等しい」ことがわかります。・2組の角の大きさが等しい
・2組の辺の比とその間の角の大きさが等しい
直角三角形の場合は1つの角の大きさが90°で確定しているため、残り1つの鋭角の角度を決定するだけでそれに対応して三角形の3辺の比も決定されるということになります。
この直角三角形の鋭角と3辺の比の関係を関数化したものが「三角関数」です。
正弦(sin)・余弦(cos)・正接(tan)
正弦(sin)・余弦(cos)・正接(tan)は直角三角形の鋭角の角度から3辺の比を求める関数です。
鋭角の角度をΘとして以下のとおりに定義されています。
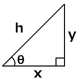 正弦(sin)・余弦(cos)を使うことで斜辺の長さとその角度から幅と高さを得ることができます。
正弦(sin)・余弦(cos)を使うことで斜辺の長さとその角度から幅と高さを得ることができます。
この計算式は地形の測量・ベクトルの座標計算・ゲームキャラクターの移動など様々な場面で活用できます。
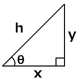 正接(tan)は斜辺の角度と高さから幅を、斜辺の角度と幅から高さを得ることができます。
正接(tan)は斜辺の角度と高さから幅を、斜辺の角度と幅から高さを得ることができます。
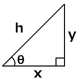
鋭角の角度をΘとして以下のとおりに定義されています。
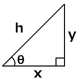
正弦 : sinΘ = y / h
余弦 : cosΘ = x / h
正接 : tanΘ = y / x
余弦 : cosΘ = x / h
正接 : tanΘ = y / x
三角関数の具体的な使い方
この計算式は地形の測量・ベクトルの座標計算・ゲームキャラクターの移動など様々な場面で活用できます。
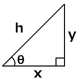
x = cosΘ × h
y = sinΘ × h
y = sinΘ × h
[例] 30°の勾配の斜面を150メートル進んだ場合の水平方向・垂直方向への移動距離を求める。
水平距離 = cos 30° × 150
垂直距離 = sin 30° × 150
cos 30°= 0.866...
sin 30°= 0.5
なので
水平距離 = 0.866 × 150 = 129.9...
垂直距離 = 0.5 × 150 = 75
よって、30°の勾配の斜面を150メートル進むと水平に約130メートル、垂直に75メートル移動する。
垂直距離 = sin 30° × 150
cos 30°= 0.866...
sin 30°= 0.5
なので
水平距離 = 0.866 × 150 = 129.9...
垂直距離 = 0.5 × 150 = 75
よって、30°の勾配の斜面を150メートル進むと水平に約130メートル、垂直に75メートル移動する。
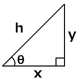
x = y ÷ tanΘ
y = x × tanΘ
y = x × tanΘ
[例] ボールを30°の角度で水平方向に130メートル投げた時のボールの垂直距離を求める
垂直距離 = 130 × tan 30°
tan 30°= 0.577...なので
垂直距離 = 130 × 0.577 = 75.01
よって、ボールを30°の角度で水平方向に130メートル投げると垂直距離は約75メートル。
tan 30°= 0.577...なので
垂直距離 = 130 × 0.577 = 75.01
よって、ボールを30°の角度で水平方向に130メートル投げると垂直距離は約75メートル。
[例] ボールを30°の角度で垂直方向に75メートル投げた時のボールの水平距離を求める
水平距離 = 75 ÷ tan 30°
tan 30°= 0.577...なので
水平距離 = 75 ÷ 0.577 = 129.98...
よって、ボールを30°の角度で垂直方向に75メートル投げると水平距離は約130メートル。
tan 30°= 0.577...なので
水平距離 = 75 ÷ 0.577 = 129.98...
よって、ボールを30°の角度で垂直方向に75メートル投げると水平距離は約130メートル。
関連コンテンツ
角度を表す単位である「度」と「ラジアン」を相互変換するツールと変換計算式の解説。